mirror of
https://github.com/heqin-zhu/algorithm.git
synced 2024-03-22 13:30:46 +08:00
82 lines
7.5 KiB
Markdown
82 lines
7.5 KiB
Markdown
# String Matching algorithm
|
|
|
|

|
|
|
|
## Rabin-Karp
|
|
We can view a string of k characters (digits) as a length-k decimal number. E.g., the string “31425” corresponds to the decimal number 31,425.
|
|
- Given a pattern P [1..m], let p denote the corresponding decimal value.
|
|
- Given a text T [1..n], let 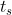 denote the decimal value of the length-m substring T [(s+1)..(s+m)] for s=0,1,…,(n-m).
|
|
- let `d` be the radix of num, thus ))
|
|
- 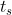 = p iff T [(s+1)..(s+m)] = P [1..m].
|
|
- p can be computed in O(m) time. p = P[m] + d\*(P[m-1] + d\*(P[m-2]+…)).
|
|
- t0 can similarly be computed in O(m) time.
|
|
- Other  can be computed in O(n-m) time since 
|
|
t_{s+1} = d*(t_s-d^{m-1} * T[s+1])+T[s+m+1]
|
|
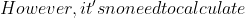t_{s+1}&space;10.&space;Generally,&space;d\*q&space;should&space;fit&space;within&space;one&space;computer&space;word.&space;We&space;firstly&space;caculate&space;t0&space;mod&space;q.&space;Then,&space;for&space;every)t_i (i>1)
|
|
t_{i-1} = T[i+m-1] + 10*T[i+m-2]+\ldots+10^{m-1}*T[i-1]
|
|
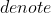 d' = d^{m-1}\ mod\ q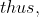
|
|
\begin{aligned}
|
|
t_i &= (t_{i-1} - d^{m-1}*T[i-1]) * d + T[i+m]\\
|
|
&\equiv (t_{i-1} - d^{m-1}*T[i-1]) * d + T[i+m] (mod\ q)\\
|
|
&\equiv (t_{i-1}- ( d^{m-1} mod \ q) *T[i-1]) * d + T[i+m] (mod\ q)\\
|
|
&\equiv (t_{i-1}- d'*T[i-1]) * d + T[i+m] (mod\ q)
|
|
\end{aligned}
|
|
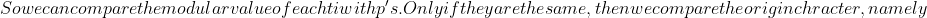T[i],T[i+1],\ldots,T[i+m-1],&space;and&space;the&space;worst&space;case&space;is&space;O((n-m+1)\*m)&space;**Problem:&space;this&space;is&space;assuming&space;p&space;and&space;ts&space;are&space;small&space;numbers.&space;They&space;may&space;be&space;too&space;large&space;to&space;work&space;with&space;easily.**&space;##&space;FSM&space;A&space;FSM&space;can&space;be&space;represented&space;as&space;(Q,q0,A,S,C),&space;where&space;-&space;Q&space;is&space;the&space;set&space;of&space;all&space;states&space;-&space;q0&space;is&space;the&space;start&space;state&space;-)A\in Q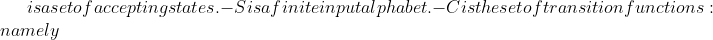q_j = c(s,q_i)$.
|
|
|
|
Given a pattern string S, we can build a FSM for string matching.
|
|
Assume S has m chars, and there should be m+1 states. One is for the begin state, and the others are for matching state of each position of S.
|
|
|
|
Once we have built the FSM, we can run it on any input string.
|
|
## KMP
|
|
>Knuth-Morris-Pratt method
|
|
|
|
The idea is inspired by FSM. We can avoid computing the transition functions. Instead, we compute a prefix functi`Next` on P in O(m) time, and Next has only m entries.
|
|
> Prefix funtion stores info about how the pattern matches against shifts of itself.
|
|
|
|
- String w is a prefix of string x, if x=wy for some string y
|
|
- String w is a suffix of string x, if x=yw for some string y
|
|
- The k-character prefix of the pattern P [1..m] denoted by Pk.
|
|
- Given that pattern prefix P [1..q] matches text characters T [(s+1)..(s+q)], what is the least shift s'> s such that P [1..k] = T [(s'+1)..(s'+k)] where s'+k=s+q?
|
|
- At the new shift s', no need to compare the first k characters of P with corresponding characters of T.
|
|
Method: For prefix pi, find the longest proper prefix of pi that is also a suffix of pi.
|
|
next[q] = max{k|k\<q and pk is a suffix of pq}
|
|
|
|
For example: p = ababaca, for p5 = ababa, Next[5] = 3. Namely p3=aba is the longest prefix of p that is also a suffix of p5.
|
|
|
|
Time approximation: finding prefix function `next` take O(m), matching takes O(m+n)
|
|
|
|
## Boyer-Moore
|
|
- The longer the pattern is, the faster it works.
|
|
- Starts from the end of pattern, while KMP starts from the beginning.
|
|
- Works best for character string, while KMP works best for binary string.
|
|
- KMP and Boyer-Moore
|
|
- Preprocessing existing patterns.
|
|
- Searching patterns in input strings.
|
|
## Sunday
|
|
### features
|
|
- simplification of the Boyer-Moore algorithm;
|
|
- uses only the bad-character shift;
|
|
- easy to implement;
|
|
- preprocessing phase in O(m+sigma) time and O(sigma) space complexity;
|
|
- searching phase in O(mn) time complexity;
|
|
- very fast in practice for short patterns and large alphabets.
|
|
### description
|
|
The Quick Search algorithm uses only the bad-character shift table (see chapter Boyer-Moore algorithm). After an attempt where the window is positioned on the text factor y[j .. j+m-1], the length of the shift is at least equal to one. So, the character y[j+m] is necessarily involved in the next attempt, and thus can be used for the bad-character shift of the current attempt.
|
|
|
|
The bad-character shift of the present algorithm is slightly modified to take into account the last character of x as follows: for c in Sigma, qsBc[c]=min{i : 0 < i leq m and x[m-i]=c} if c occurs in x, m+1 otherwise (thanks to Darko Brljak).
|
|
|
|
The preprocessing phase is in O(m+sigma) time and O(sigma) space complexity.
|
|
|
|
During the searching phase the comparisons between pattern and text characters during each attempt can be done in any order. The searching phase has a quadratic worst case time complexity but it has a good practical behaviour.
|
|
|
|
For instance,
|
|

|
|
|
|
In this example, t0, ..., t4 = a b c a b is the current text window that is compared with the pattern. Its suffix a b has matched, but the comparison c-a causes a mismatch. The bad-character heuristics of the Boyer-Moore algorithm (a) uses the "bad" text character c to determine the shift distance. The Horspool algorithm (b) uses the rightmost character b of the current text window. The Sunday algorithm (c) uses the character directly right of the text window, namely d in this example. Since d does not occur in the pattern at all, the pattern can be shifted past this position.
|
|
|
|
|
|
# Reference:
|
|
1. Xuyun, ppt, String matching
|
|
2. [Sunday-algorithm](http://www.inf.fh-flensburg.de/lang/algorithmen/pattern/sunday.htm)
|
|
3. GeeksforGeeks, [KMP Algorithm](https://www.geeksforgeeks.org/kmp-algorithm-for-pattern-searching/)
|