---
title: 『算法』概述
categories: 数据结构与算法
tags: [算法]
keywords:
mathjax: true
top:
---
- [1. 算法](#1-算法)
- [2. 可以解决哪些类型的问题](#2-可以解决哪些类型的问题)
- [3. 算法分析](#3-算法分析)
- [4. 算法设计](#4-算法设计)
- [4.1. 分治(divide and conquer)](#41-分治divide-and-conquer)
- [5. 递归式](#5-递归式)
- [5.1. 代换法](#51-代换法)
- [5.1.1. 步骤](#511-步骤)
- [5.1.2. 例子](#512-例子)
- [5.1.3. 放缩](#513-放缩)
- [5.1.4. 改变变量](#514-改变变量)
- [5.2. 递归树](#52-递归树)
- [5.3. 主方法(master method)](#53-主方法master-method)
- [5.3.1. 记忆](#531-记忆)
- [5.3.2. 证明](#532-证明)
- [5.3.2.1. 证明当 n 为 b 的正合幂时成立](#5321-证明当-n-为-b-的正合幂时成立)
- [5.3.2.2. 分析扩展至所有正整数 n 都成立](#5322-分析扩展至所有正整数-n-都成立)
- [6. 随机算法](#6-随机算法)
- [6.1. 随机排列数组(shuffle)](#61-随机排列数组shuffle)
- [6.1.1. PERMUTE-BY-SORTING](#611-permute-by-sorting)
- [6.1.2. RANDOMIZE-IN-PLACE](#612-randomize-in-place)
- [7. 组合方程的近似算法](#7-组合方程的近似算法)
- [8. 概率分析与指示器变量例子](#8-概率分析与指示器变量例子)
- [8.1. 球与盒子](#81-球与盒子)
- [8.2. 序列](#82-序列)
- [9. 摊还分析](#9-摊还分析)
- [9.1. 聚合分析(aggregate analysis)](#91-聚合分析aggregate-analysis)
- [9.2. 核算法 (accounting method)](#92-核算法-accounting-method)
- [9.3. 势能法(potential method)](#93-势能法potential-method)
# 1. 算法
定义良好的计算过程,取输入,并产生输出. 即算法是一系列的计算步骤,将输入数据转化为输出结果
# 2. 可以解决哪些类型的问题
* 大数据的存储,以及开发出进行这方面数据分析的工具
* 网络数据的传输,寻路, 搜索
* 电子商务密码, (数值算法,数论)
* 资源分配,最大效益
* ...
# 3. 算法分析
衡量算法的优劣

* 
* 最坏情况, 平均情况
* 增长的量级,O(logn),&space;O(n),&space;O(n^k),&space;O(a^n))
# 4. 算法设计
## 4.1. 分治(divide and conquer)
结构上是递归的,
步骤: 分解,解决, 合并
eg 快排,归并排序
# 5. 递归式
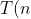&space;=&space;aT(\frac{n}&space;{b})+f(n))
## 5.1. 代换法
### 5.1.1. 步骤
* 猜测解的形式
* 用数学归纳法找出常数
### 5.1.2. 例子
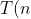&space;=&space;2T(\frac{n}&space;{2})+n)
猜测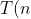&space;=&space;O(nlogn))
证明 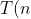\leqslant&space;cnlogn)
归纳奠基 n=2,3
归纳假设 &space;\leqslant&space;\frac{cn}{2})
递归
&space;&\leqslant&space;2c\frac{n}{2}log(\frac{n}{2})&space;+&space;n&space;\leqslant&space;cnlog(\frac{n}{2})&space;\\&space;\end{aligned}&space;)
### 5.1.3. 放缩
对于 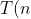&space;=&space;2T(\frac{cn}{2})&space;+&space;1)
如果 直接猜测 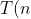&space;=&space;O&space;(n)) 不能证明,
而且不要猜测更高的界 )
可以放缩为 n-b
### 5.1.4. 改变变量
对于 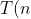&space;=&space;2T(\sqrt{n})+logn)
可以 令 `m = logn`, 得到
&space;=&space;2T(m^{\frac{m}{2}})&space;+&space;m)
令 &space;=&space;T(2^m))
得到 &space;=&space;2S(\frac{m}{2})&space;+&space;m)
## 5.2. 递归树
例如 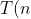&space;=&space;3T(\frac{n}{4})&space;+&space;c&space;n^2)
不妨假设 n 为4的幂, 则有如下递归树

每个结点是代价, 将每层加起来即可
## 5.3. 主方法(master method)
对于 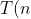&space;=&space;aT(\frac{n}&space;{b})+f(n))
=\begin{cases}&space;\Theta(n^{log_b&space;a}),\quad&space;f(n)=O(n^{&space;{log_b&space;a}-\epsilon})&space;\\&space;\Theta(n^{log_b&space;a}logn),\quad&space;f(n)=\Theta(n^{log_b&space;a})&space;\\&space;\Theta(f(n)),\quad&space;f(n)=\Omega(n^{&space;{log_b&space;a}+&space;\epsilon}),af(\frac{n}{b})\leqslant&space;cf(n)&space;\\&space;\qquad&space;\qquad&space;\quad&space;\text{Constantc<1,VariablenArbitrarily-large}&space;\\&space;unknown,&space;\quad&space;others&space;\end{cases}&space;\end{aligned}&space;)
### 5.3.1. 记忆
直观上, 比较  和 ), 谁大就是谁,
这里的大是多项式上的比较, 即比较次数, 而不是渐近上的
比如  与  渐近上后者大, 但多项式上是不能比较的
### 5.3.2. 证明
#### 5.3.2.1. 证明当 n 为 b 的正合幂时成立
* 用递归树可以得到 总代价为 )
* 决定上式的渐近界
* 结合前两点
#### 5.3.2.2. 分析扩展至所有正整数 n 都成立
主要是应用数学技巧来解决 floor, ceiling 函数的处理问题
# 6. 随机算法
## 6.1. 随机排列数组(shuffle)
### 6.1.1. PERMUTE-BY-SORTING
给出初始数组, eg A={1,2,3}, 选择随机的优先级 P={16,4,10}
则得出 B={2,3,1},因为第二个(2)优先级最小, 为4, 接着第三个,最后第1个.
优先级数组的产生, 一般在 RANDOM(1,n^3), 这样优先级各不相同的概率至少为 1-1/n
由于要排序优先级数组, 所以时间复杂度 )
如果优先级唯一, 则此算法可以 shuffle 数组
应证明 同样排列的概率是 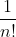
### 6.1.2. RANDOMIZE-IN-PLACE
```python
# arr: array to be shuffled
n = len(arr)
for i in range(n):
swap(arr[i],arr[random(i,n-1)])
```
时间复杂度 )
证明
定义循环不变式: 对每个可能的  排列, 其在 arr[1..i-1] 中的概率为 
初始化: i=1 成立
保持 : 假设 在第 i-1 次迭代之前,成立, 证明在第 i 次迭代之后, 仍然成立,
终止: 在 结束后, i=n+1, 得到 概率为 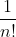
# 7. 组合方程的近似算法
* Stiring's approximation: ^n)
* 对于 , 有 
* 对于 , 有 ^{\frac{1}{n}}+\frac{n}{2})
# 8. 概率分析与指示器变量例子
## 8.1. 球与盒子
把相同的秋随机投到 b 个盒子里,问在每个盒子里至少有一个球之前,平均至少要投多少个球?
称投入一个空盒为击中, 即求取得 b 次击中的概率
设投 n 次, 称第 i 个阶段包括第 i-1 次击中到 第 i 次击中的球, 则第 i 次击中的概率为 
用 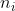表示第 i 阶段的投球数,则 
且 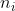服从几何分布, =\frac{b}{b-i+1}),
则由期望的线性性,
=E(\sum_{i=1}^b&space;n_i)=\sum_{i=1}^b&space;E(n_i)=\sum_{i=1}^b&space;\frac{b}{b-i+1}=b\sum_{i=1}^b&space;\frac{1}{i}=b(lnb+O(1))&space;)
这个问题又被称为 赠券收集者问题(coupon collector's problem),即集齐 b 种不同的赠券,在随机情况下平均需要买 blnb 张
## 8.2. 序列
抛 n 次硬币, 期望看到的连续正面的次数
答案是 )
记 长度至少为 k 的正面序列开始与第 i 次抛, 由于独立, 所有 k 次抛掷都是正面的 概率为
=\frac{1}{2^k}),对于 




# 9. 摊还分析
## 9.1. 聚合分析(aggregate analysis)
一个 n 个操作的序列最坏情况下花费的总时间为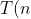), 则在最坏情况下, 每个操作的摊还代价为 }{n})
如栈中的 push, pop 操作都是 ), 增加一个新操作 `multipop`,
```python
def multipop(stk,k):
while not stk.empty() and k>0:
stk.pop()
k-=1
```
multipop 的时间复杂度为 min(stk.size,k), 最坏情况为 ), 则 n 个包含 push pop multipop 的操作列的最坏情况是 ), 并不是这样, 注意到, 必须栈中有元素, 再 pop, 所以 push 操作与pop 操作(包含 multipop中的pop), 个数相当, 所以 实际上应为 ), 每个操作的摊还代价 为)
## 9.2. 核算法 (accounting method)
对不同操作赋予不同费用 cost (称为摊还代价 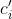), 可能多于或者少于其实际代价 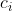
当 , 将 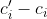( `credit`) 存入数据结构中的特定对象.. 对于后续 
势能释放用来支付未来操作的代价, 势能是整个数据结构的, 不是特定对象的(核算法是).
数据结构 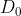为初始状态, 依次 执行 n 个操作 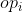进行势能转换 ,&space;i=1,2,\ldots,n) , 各操作代价为 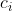
势函数 , )即为 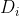的势
则第 i 个操作的摊还代价
-\Phi(D_{i-1}))
则
-\Phi(D_0))
如果定义一个势函数\geqslant\Phi(D_0)), 则总摊还代价给出了实际代价的一个上界
可以简单地以 =0)
例如栈操作,
设空栈为 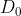, 势函数定义为栈的元素数
对于push, -\Phi(D_0)=1)
则 -\Phi(D_0)&space;=&space;c+1&space;=&space;2)
对于 multipop, -\Phi(D_0)=-&space;min(k,s))
则 &space;=&space;0)
同理 pop 的摊还代价也是0, 则总摊还代价的上界(最坏情况) 为 )