12 KiB
- 60. n 个骰子的点数
- 61. 扑克牌顺子
- 62. 圆圈中最后剩下的数
- 63. 股票的最大利润
- 64. 求 1+2+3+...+n
- 65. 不用加减乘除做加法
- 66. 构建乘积数组
- 67. 把字符串转换成整数
- 68. 树中两个节点的最低公共祖先
60. n 个骰子的点数
题目描述
把 n 个骰子仍在地上,求点数和为 s 的概率。
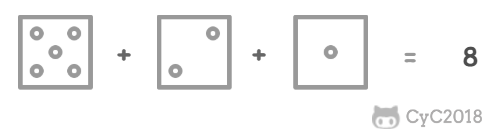
解题思路
动态规划
使用一个二维数组 dp 存储点数出现的次数,其中 dp[i][j] 表示前 i 个骰子产生点数 j 的次数。
空间复杂度:O(N2)
public List<Map.Entry<Integer, Double>> dicesSum(int n) {
final int face = 6;
final int pointNum = face * n;
long[][] dp = new long[n + 1][pointNum + 1];
for (int i = 1; i <= face; i++)
dp[1][i] = 1;
for (int i = 2; i <= n; i++)
for (int j = i; j <= pointNum; j++) /* 使用 i 个骰子最小点数为 i */
for (int k = 1; k <= face && k <= j; k++)
dp[i][j] += dp[i - 1][j - k];
final double totalNum = Math.pow(6, n);
List<Map.Entry<Integer, Double>> ret = new ArrayList<>();
for (int i = n; i <= pointNum; i++)
ret.add(new AbstractMap.SimpleEntry<>(i, dp[n][i] / totalNum));
return ret;
}
动态规划 + 旋转数组
空间复杂度:O(N)
public List<Map.Entry<Integer, Double>> dicesSum(int n) {
final int face = 6;
final int pointNum = face * n;
long[][] dp = new long[2][pointNum + 1];
for (int i = 1; i <= face; i++)
dp[0][i] = 1;
int flag = 1; /* 旋转标记 */
for (int i = 2; i <= n; i++, flag = 1 - flag) {
for (int j = 0; j <= pointNum; j++)
dp[flag][j] = 0; /* 旋转数组清零 */
for (int j = i; j <= pointNum; j++)
for (int k = 1; k <= face && k <= j; k++)
dp[flag][j] += dp[1 - flag][j - k];
}
final double totalNum = Math.pow(6, n);
List<Map.Entry<Integer, Double>> ret = new ArrayList<>();
for (int i = n; i <= pointNum; i++)
ret.add(new AbstractMap.SimpleEntry<>(i, dp[1 - flag][i] / totalNum));
return ret;
}
61. 扑克牌顺子
题目描述
五张牌,其中大小鬼为癞子,牌面为 0。判断这五张牌是否能组成顺子。

解题思路
public boolean isContinuous(int[] nums) {
if (nums.length < 5)
return false;
Arrays.sort(nums);
// 统计癞子数量
int cnt = 0;
for (int num : nums)
if (num == 0)
cnt++;
// 使用癞子去补全不连续的顺子
for (int i = cnt; i < nums.length - 1; i++) {
if (nums[i + 1] == nums[i])
return false;
cnt -= nums[i + 1] - nums[i] - 1;
}
return cnt >= 0;
}
62. 圆圈中最后剩下的数
题目描述
让小朋友们围成一个大圈。然后,随机指定一个数 m,让编号为 0 的小朋友开始报数。每次喊到 m-1 的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续 0...m-1 报数 .... 这样下去 .... 直到剩下最后一个小朋友,可以不用表演。
解题思路
约瑟夫环,圆圈长度为 n 的解可以看成长度为 n-1 的解再加上报数的长度 m。因为是圆圈,所以最后需要对 n 取余。
public int LastRemaining_Solution(int n, int m) {
if (n == 0) /* 特殊输入的处理 */
return -1;
if (n == 1) /* 递归返回条件 */
return 0;
return (LastRemaining_Solution(n - 1, m) + m) % n;
}
63. 股票的最大利润
题目描述
可以有一次买入和一次卖出,买入必须在前。求最大收益。
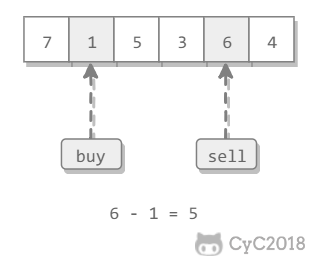
解题思路
使用贪心策略,假设第 i 轮进行卖出操作,买入操作价格应该在 i 之前并且价格最低。
public int maxProfit(int[] prices) {
if (prices == null || prices.length == 0)
return 0;
int soFarMin = prices[0];
int maxProfit = 0;
for (int i = 1; i < prices.length; i++) {
soFarMin = Math.min(soFarMin, prices[i]);
maxProfit = Math.max(maxProfit, prices[i] - soFarMin);
}
return maxProfit;
}
64. 求 1+2+3+...+n
题目描述
要求不能使用乘除法、for、while、if、else、switch、case 等关键字及条件判断语句 A ? B : C。
解题思路
使用递归解法最重要的是指定返回条件,但是本题无法直接使用 if 语句来指定返回条件。
条件与 && 具有短路原则,即在第一个条件语句为 false 的情况下不会去执行第二个条件语句。利用这一特性,将递归的返回条件取非然后作为 && 的第一个条件语句,递归的主体转换为第二个条件语句,那么当递归的返回条件为 true 的情况下就不会执行递归的主体部分,递归返回。
本题的递归返回条件为 n <= 0,取非后就是 n > 0;递归的主体部分为 sum += Sum_Solution(n - 1),转换为条件语句后就是 (sum += Sum_Solution(n - 1)) > 0。
public int Sum_Solution(int n) {
int sum = n;
boolean b = (n > 0) && ((sum += Sum_Solution(n - 1)) > 0);
return sum;
}
65. 不用加减乘除做加法
题目描述
写一个函数,求两个整数之和,要求不得使用 +、-、*、/ 四则运算符号。
解题思路
a ^ b 表示没有考虑进位的情况下两数的和,(a & b) << 1 就是进位。
递归会终止的原因是 (a & b) << 1 最右边会多一个 0,那么继续递归,进位最右边的 0 会慢慢增多,最后进位会变为 0,递归终止。
public int Add(int a, int b) {
return b == 0 ? a : Add(a ^ b, (a & b) << 1);
}
66. 构建乘积数组
题目描述
给定一个数组 A[0, 1,..., n-1],请构建一个数组 B[0, 1,..., n-1],其中 B 中的元素 B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。要求不能使用除法。
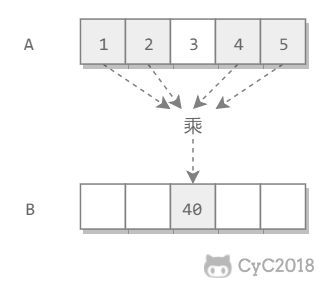
解题思路
public int[] multiply(int[] A) {
int n = A.length;
int[] B = new int[n];
for (int i = 0, product = 1; i < n; product *= A[i], i++) /* 从左往右累乘 */
B[i] = product;
for (int i = n - 1, product = 1; i >= 0; product *= A[i], i--) /* 从右往左累乘 */
B[i] *= product;
return B;
}
67. 把字符串转换成整数
题目描述
将一个字符串转换成一个整数,字符串不是一个合法的数值则返回 0,要求不能使用字符串转换整数的库函数。
Iuput:
+2147483647
1a33
Output:
2147483647
0
解题思路
public int StrToInt(String str) {
if (str == null || str.length() == 0)
return 0;
boolean isNegative = str.charAt(0) == '-';
int ret = 0;
for (int i = 0; i < str.length(); i++) {
char c = str.charAt(i);
if (i == 0 && (c == '+' || c == '-')) /* 符号判定 */
continue;
if (c < '0' || c > '9') /* 非法输入 */
return 0;
ret = ret * 10 + (c - '0');
}
return isNegative ? -ret : ret;
}
68. 树中两个节点的最低公共祖先
解题思路
二叉查找树
Leetcode : 235. Lowest Common Ancestor of a Binary Search Tree
二叉查找树中,两个节点 p, q 的公共祖先 root 满足 root.val >= p.val && root.val <= q.val。
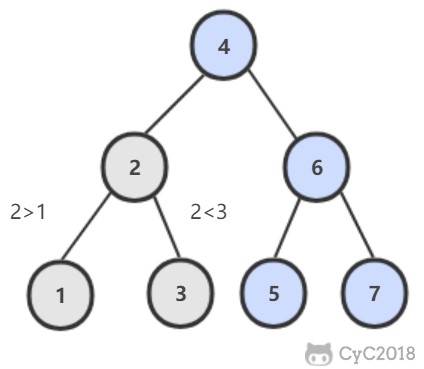
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null)
return root;
if (root.val > p.val && root.val > q.val)
return lowestCommonAncestor(root.left, p, q);
if (root.val < p.val && root.val < q.val)
return lowestCommonAncestor(root.right, p, q);
return root;
}
普通二叉树
Leetcode : 236. Lowest Common Ancestor of a Binary Tree
在左右子树中查找是否存在 p 或者 q,如果 p 和 q 分别在两个子树中,那么就说明根节点就是最低公共祖先。
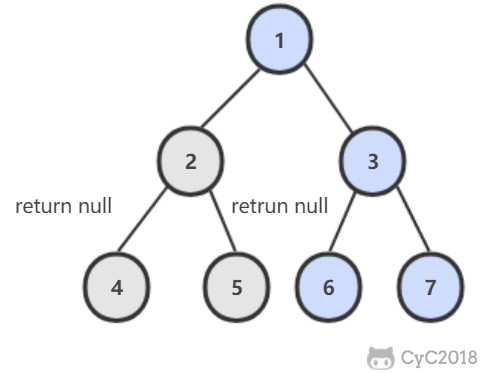
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q)
return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
return left == null ? right : right == null ? left : root;
}
微信公众号
更多精彩内容将发布在微信公众号 CyC2018 上,你也可以在公众号后台和我交流学习和求职相关的问题。另外,公众号提供了该项目的 PDF 等离线阅读版本,后台回复 "下载" 即可领取。公众号也提供了一份技术面试复习大纲,不仅系统整理了面试知识点,而且标注了各个知识点的重要程度,从而帮你理清多而杂的面试知识点,后台回复 "大纲" 即可领取。我基本是按照这个大纲来进行复习的,对我拿到了 BAT 头条等 Offer 起到很大的帮助。你们完全可以和我一样根据大纲上列的知识点来进行复习,就不用看很多不重要的内容,也可以知道哪些内容很重要从而多安排一些复习时间。
