diff --git a/notes/Leetcode 题解.md b/notes/Leetcode 题解.md
index 8ba46162..cf67cdca 100644
--- a/notes/Leetcode 题解.md
+++ b/notes/Leetcode 题解.md
@@ -1820,7 +1820,7 @@ public int minPathSum(int[][] grid) {
定义一个数组 dp 存储上楼梯的方法数(为了方便讨论,数组下标从 1 开始),dp[i] 表示走到第 i 个楼梯的方法数目。第 i 个楼梯可以从第 i-1 和 i-2 个楼梯再走一步到达,走到第 i 个楼梯的方法数为走到第 i-1 和第 i-2 个楼梯的方法数之和。
-
+
dp[N] 即为所求。
@@ -1849,7 +1849,7 @@ public int climbStairs(int n) {
第 i 年成熟的牛的数量为:
-
+
**强盗抢劫**
@@ -1859,7 +1859,7 @@ public int climbStairs(int n) {
定义 dp 数组用来存储最大的抢劫量,其中 dp[i] 表示抢到第 i 个住户时的最大抢劫量。由于不能抢劫邻近住户,因此如果抢劫了第 i 个住户那么只能抢劫 i - 2 和 i - 3 的住户,所以
-
+
O(n) 空间复杂度实现方法:
@@ -1938,7 +1938,7 @@ private int rob(int[] nums, int s, int e) {
综上所述,错误装信数量方式数量为:
-
+
dp[N] 即为所求。
@@ -1954,7 +1954,7 @@ dp[N] 即为所求。
因为在求 dp[n] 时可能无法找到一个满足条件的递增子序列,此时 {Sn} 就构成了递增子序列,因此需要对前面的求解方程做修改,令 dp[n] 最小为 1,即:
-
+
对于一个长度为 N 的序列,最长子序列并不一定会以 SN 为结尾,因此 dp[N] 不是序列的最长递增子序列的长度,需要遍历 dp 数组找出最大值才是所要的结果,即 max{ dp[i] | 1 <= i <= N} 即为所求。
@@ -2050,7 +2050,7 @@ public int wiggleMaxLength(int[] nums) {
综上,最长公共子系列的状态转移方程为:
-
+
对于长度为 N 的序列 S1 和 长度为 M 的序列 S2,dp[N][M] 就是序列 S1 和序列 S2 的最长公共子序列长度。
@@ -2087,7 +2087,7 @@ public int lengthOfLCS(int[] nums1, int[] nums2) {
综上,0-1 背包的状态转移方程为:
-
+
```java
public int knapsack(int W, int N, int[] weights, int[] values) {
@@ -2111,7 +2111,7 @@ public int knapsack(int W, int N, int[] weights, int[] values) {
在程序实现时可以对 0-1 背包做优化。观察状态转移方程可以知道,前 i 件物品的状态仅由前 i-1 件物品的状态有关,因此可以将 dp 定义为一维数组,其中 dp[j] 既可以表示 dp[i-1][j] 也可以表示 dp[i][j]。此时,
-
+
因为 dp[j-w] 表示 dp[i-1][j-w],因此不能先求 dp[i][j-w] 防止将 dp[i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w],在程序实现时需要按倒序来循环求解。
diff --git a/notes/数据库系统原理.md b/notes/数据库系统原理.md
index a38880b7..2373c605 100644
--- a/notes/数据库系统原理.md
+++ b/notes/数据库系统原理.md
@@ -216,23 +216,23 @@ MySQL InnoDB 采用的是两阶段锁协议。在事务执行过程中,随时
**分解前**
-
+
-
+
**分解后**
-
+
-
+
-
+
-
+
-
+
@@ -250,15 +250,15 @@ MySQL InnoDB 采用的是两阶段锁协议。在事务执行过程中,随时
关系模式 STC(Sname, Tname, Cname, Grade),其中四个属性分别为学生姓名、教师姓名、课程名和成绩。有以下函数依赖:
-
+
-
+
-
+
-
+
-
+
分解成 SC(Sname, Cname, Grade) 和 ST(Sname, Tname),对于 ST,属性之间是多对多关系,无函数依赖。
diff --git a/notes/算法.md b/notes/算法.md
index 5c57bf1e..bbe55ffb 100644
--- a/notes/算法.md
+++ b/notes/算法.md
@@ -93,11 +93,11 @@
指数函数可以转换为线性函数,从而在函数图像上显示的更直观。例如
-
+
可以在其两端同时取对数,得到:
-
+
diff --git a/notes/计算机操作系统.md b/notes/计算机操作系统.md
index 6a85d3ab..86d9ddbb 100644
--- a/notes/计算机操作系统.md
+++ b/notes/计算机操作系统.md
@@ -723,7 +723,7 @@ void test(i) { // 尝试拿起两把筷子
举例:一个系统为某进程分配了三个物理块,并有如下页面引用序列:
-
+
进程运行时,先将 7,0,1 三个页面装入内存。当进程要访问页面 2 时,产生缺页中断,会将页面 7 换出,因为页面 7 再次被访问的时间最长。
@@ -739,7 +739,7 @@ void test(i) { // 尝试拿起两把筷子
可以用栈来实现该算法,栈中存储页面的页面号。当进程访问一个页面时,将该页面的页面号从栈移除,并将它压入栈顶。这样,最近被访问的页面的页面号总是在栈顶,而最近最久未使用的页面的页面号总是在栈底。
-
+
diff --git a/notes/计算机网络.md b/notes/计算机网络.md
index 7b095a2a..99255071 100644
--- a/notes/计算机网络.md
+++ b/notes/计算机网络.md
@@ -161,7 +161,7 @@
主机或路由器发送数据帧所需要的时间。
-
+
其中 l 表示数据帧的长度,v 表示发送速率。
@@ -169,7 +169,7 @@
电磁波在信道中传播一定的距离需要花费的时间,电磁波传播速度接近光速。
-
+
其中 l 表示信道长度,v 表示电磁波在信道上的传播速率。
@@ -264,7 +264,7 @@ TCP/IP 协议族是一种沙漏形状,中间小两边大,IP 协议在其中
为每个用户分配 m bit 的码片,并且所有的码片正交,对于任意两个码片 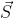 和
和 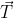 有
-
有
-
+
为了方便,取 m=8,设码片 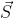 为 00011011。在拥有该码片的用户发送比特 1 时就发送该码片,发送比特 0 时就发送该码片的反码 11100100。
@@ -272,9 +272,9 @@ TCP/IP 协议族是一种沙漏形状,中间小两边大,IP 协议在其中
为 00011011。在拥有该码片的用户发送比特 1 时就发送该码片,发送比特 0 时就发送该码片的反码 11100100。
@@ -272,9 +272,9 @@ TCP/IP 协议族是一种沙漏形状,中间小两边大,IP 协议在其中
-
+
-其中 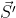 为
为 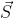 的反码。
的反码。
+其中 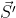 为
为 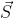 的反码。
利用上面的式子我们知道,当接收端使用码片
的反码。
利用上面的式子我们知道,当接收端使用码片 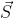 对接收到的数据进行内积运算时,结果为 0 的是其它用户发送的数据,结果为 1 的是用户发送的比特 1,结果为 -1 的是用户发送的比特 0。
@@ -689,11 +689,11 @@ TCP 使用超时重传来实现可靠传输:如果一个已经发送的报文
一个报文段从发送再到接收到确认所经过的时间称为往返时间 RTT,加权平均往返时间 RTTs 计算如下:
-
对接收到的数据进行内积运算时,结果为 0 的是其它用户发送的数据,结果为 1 的是用户发送的比特 1,结果为 -1 的是用户发送的比特 0。
@@ -689,11 +689,11 @@ TCP 使用超时重传来实现可靠传输:如果一个已经发送的报文
一个报文段从发送再到接收到确认所经过的时间称为往返时间 RTT,加权平均往返时间 RTTs 计算如下:
-
+
超时时间 RTO 应该略大于 RRTs,TCP 使用的超时时间计算如下:
-
+
其中 RTTd 为偏差,它与新的 RRT 和 RRTs 有关。



