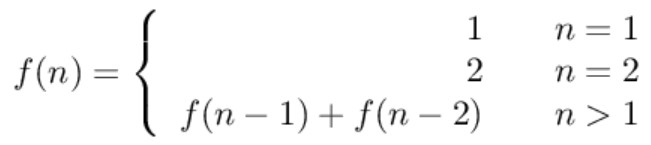diff --git a/docs/notes/剑指 Offer 题解 - 10~19.md b/docs/notes/剑指 Offer 题解 - 10~19.md
index 598ad80e..f913b5da 100644
--- a/docs/notes/剑指 Offer 题解 - 10~19.md
+++ b/docs/notes/剑指 Offer 题解 - 10~19.md
@@ -65,7 +65,7 @@ public int Fibonacci(int n) {
}
```
-由于待求解的 n 小于 40,因此可以将前 40 项的结果先进行计算,之后就能以 O(1) 时间复杂度得到第 n 项的值了。
+由于待求解的 n 小于 40,因此可以将前 40 项的结果先进行计算,之后就能以 O(1) 时间复杂度得到第 n 项的值。
```java
public class Solution {
@@ -96,6 +96,20 @@ public class Solution {
## 解题思路
+当 n 为 1 时,只有一种覆盖方法:
+
+
+
+当 n 为 2 时,有两种覆盖方法:
+
+
+
+要覆盖 2\*n 的大矩形,可以先覆盖 2\*1 的矩形,再覆盖 2\*(n-1) 的矩形;或者先覆盖 2\*2 的矩形,再覆盖 2\*(n-2) 的矩形。而覆盖 2\*(n-1) 和 2\*(n-2) 的矩形可以看成子问题。该问题的递推公式如下:
+
+
+
+
+
```java
public int RectCover(int n) {
if (n <= 2)
diff --git a/docs/pics/508c6e52-9f93-44ed-b6b9-e69050e14807.jpg b/docs/pics/508c6e52-9f93-44ed-b6b9-e69050e14807.jpg
new file mode 100644
index 00000000..f7f3ca5b
Binary files /dev/null and b/docs/pics/508c6e52-9f93-44ed-b6b9-e69050e14807.jpg differ
diff --git a/docs/pics/db85a909-5e11-48b2-85d2-f003e7bb35c0.png b/docs/pics/db85a909-5e11-48b2-85d2-f003e7bb35c0.png
new file mode 100644
index 00000000..2c87f48e
Binary files /dev/null and b/docs/pics/db85a909-5e11-48b2-85d2-f003e7bb35c0.png differ
diff --git a/docs/pics/fec3ba89-115a-4cf9-b165-756757644641.png b/docs/pics/fec3ba89-115a-4cf9-b165-756757644641.png
new file mode 100644
index 00000000..1a313d2d
Binary files /dev/null and b/docs/pics/fec3ba89-115a-4cf9-b165-756757644641.png differ
diff --git a/notes/pics/508c6e52-9f93-44ed-b6b9-e69050e14807.jpg b/notes/pics/508c6e52-9f93-44ed-b6b9-e69050e14807.jpg
new file mode 100644
index 00000000..f7f3ca5b
Binary files /dev/null and b/notes/pics/508c6e52-9f93-44ed-b6b9-e69050e14807.jpg differ
diff --git a/notes/pics/db85a909-5e11-48b2-85d2-f003e7bb35c0.png b/notes/pics/db85a909-5e11-48b2-85d2-f003e7bb35c0.png
new file mode 100644
index 00000000..2c87f48e
Binary files /dev/null and b/notes/pics/db85a909-5e11-48b2-85d2-f003e7bb35c0.png differ
diff --git a/notes/pics/fec3ba89-115a-4cf9-b165-756757644641.png b/notes/pics/fec3ba89-115a-4cf9-b165-756757644641.png
new file mode 100644
index 00000000..1a313d2d
Binary files /dev/null and b/notes/pics/fec3ba89-115a-4cf9-b165-756757644641.png differ
diff --git a/notes/剑指 Offer 题解 - 10~19.md b/notes/剑指 Offer 题解 - 10~19.md
index 4a5b7c1e..741289f7 100644
--- a/notes/剑指 Offer 题解 - 10~19.md
+++ b/notes/剑指 Offer 题解 - 10~19.md
@@ -65,7 +65,7 @@ public int Fibonacci(int n) {
}
```
-由于待求解的 n 小于 40,因此可以将前 40 项的结果先进行计算,之后就能以 O(1) 时间复杂度得到第 n 项的值了。
+由于待求解的 n 小于 40,因此可以将前 40 项的结果先进行计算,之后就能以 O(1) 时间复杂度得到第 n 项的值。
```java
public class Solution {
@@ -96,6 +96,20 @@ public class Solution {
## 解题思路
+当 n 为 1 时,只有一种覆盖方法:
+
+
+
+当 n 为 2 时,有两种覆盖方法:
+
+
+
+要覆盖 2\*n 的大矩形,可以先覆盖 2\*1 的矩形,再覆盖 2\*(n-1) 的矩形;或者先覆盖 2\*2 的矩形,再覆盖 2\*(n-2) 的矩形。而覆盖 2\*(n-1) 和 2\*(n-2) 的矩形可以看成子问题。该问题的递推公式如下:
+
+
+
+
+
```java
public int RectCover(int n) {
if (n <= 2)