diff --git a/docs/notes/剑指 Offer 题解 - 10~19.md b/docs/notes/剑指 Offer 题解 - 10~19.md
index e4e4ec26..d31c19ed 100644
--- a/docs/notes/剑指 Offer 题解 - 10~19.md
+++ b/docs/notes/剑指 Offer 题解 - 10~19.md
@@ -296,7 +296,7 @@ private int minNumber(int[] nums, int l, int h) {
## 题目描述
-请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。
+判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。
例如下面的矩阵包含了一条 bfce 路径。
@@ -304,14 +304,19 @@ private int minNumber(int[] nums, int l, int h) {
## 解题思路
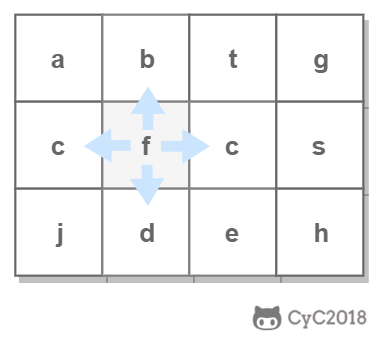
+使用回溯法(backtracking)进行求解,它是一种暴力搜索方法,通过搜索所有可能的结果来求解问题。回溯法在一次搜索结束时需要进行回溯(回退),将这一次搜索过程中设置的状态进行清除,从而开始一次新的搜索过程。例如下图示例中,从 f 开始,下一步有 4 种搜索可能,如果先搜索 b,需要将 b 标记为已经使用,防止重复使用。在这一次搜索结束之后,需要将 b 的已经使用状态清除,并搜索 c。
+
+
+
+本题的输入是数组而不是矩阵(二维数组),因此需要先将数组转换成矩阵。
+
```java
private final static int[][] next = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};
private int rows;
private int cols;
public boolean hasPath(char[] array, int rows, int cols, char[] str) {
- if (rows == 0 || cols == 0)
- return false;
+ if (rows == 0 || cols == 0) return false;
this.rows = rows;
this.cols = cols;
boolean[][] marked = new boolean[rows][cols];
@@ -320,14 +325,19 @@ public boolean hasPath(char[] array, int rows, int cols, char[] str) {
for (int j = 0; j < cols; j++)
if (backtracking(matrix, str, marked, 0, i, j))
return true;
+
return false;
}
-private boolean backtracking(char[][] matrix, char[] str, boolean[][] marked, int pathLen, int r, int c) {
- if (pathLen == str.length)
- return true;
- if (r < 0 || r >= rows || c < 0 || c >= cols || matrix[r][c] != str[pathLen] || marked[r][c])
+private boolean backtracking(char[][] matrix, char[] str,
+ boolean[][] marked, int pathLen, int r, int c) {
+
+ if (pathLen == str.length) return true;
+ if (r < 0 || r >= rows || c < 0 || c >= cols
+ || matrix[r][c] != str[pathLen] || marked[r][c]) {
+
return false;
+ }
marked[r][c] = true;
for (int[] n : next)
if (backtracking(matrix, str, marked, pathLen + 1, r + n[0], c + n[1]))
@@ -338,9 +348,9 @@ private boolean backtracking(char[][] matrix, char[] str, boolean[][] marked, in
private char[][] buildMatrix(char[] array) {
char[][] matrix = new char[rows][cols];
- for (int i = 0, idx = 0; i < rows; i++)
- for (int j = 0; j < cols; j++)
- matrix[i][j] = array[idx++];
+ for (int r = 0, idx = 0; r < rows; r++)
+ for (int c = 0; c < cols; c++)
+ matrix[r][c] = array[idx++];
return matrix;
}
```
diff --git a/docs/pics/dc964b86-7a08-4bde-a3d9-e6ddceb29f98.png b/docs/pics/dc964b86-7a08-4bde-a3d9-e6ddceb29f98.png
new file mode 100644
index 00000000..a08e6be1
Binary files /dev/null and b/docs/pics/dc964b86-7a08-4bde-a3d9-e6ddceb29f98.png differ
diff --git a/notes/pics/dc964b86-7a08-4bde-a3d9-e6ddceb29f98.png b/notes/pics/dc964b86-7a08-4bde-a3d9-e6ddceb29f98.png
new file mode 100644
index 00000000..a08e6be1
Binary files /dev/null and b/notes/pics/dc964b86-7a08-4bde-a3d9-e6ddceb29f98.png differ
diff --git a/notes/剑指 Offer 题解 - 10~19.md b/notes/剑指 Offer 题解 - 10~19.md
index 6902dddd..8bb22cd0 100644
--- a/notes/剑指 Offer 题解 - 10~19.md
+++ b/notes/剑指 Offer 题解 - 10~19.md
@@ -296,7 +296,7 @@ private int minNumber(int[] nums, int l, int h) {
## 题目描述
-请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。
+判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。
例如下面的矩阵包含了一条 bfce 路径。
@@ -304,14 +304,19 @@ private int minNumber(int[] nums, int l, int h) {
## 解题思路
+使用回溯法(backtracking)进行求解,它是一种暴力搜索方法,通过搜索所有可能的结果来求解问题。回溯法在一次搜索结束时需要进行回溯(回退),将这一次搜索过程中设置的状态进行清除,从而开始一次新的搜索过程。例如下图示例中,从 f 开始,下一步有 4 种搜索可能,如果先搜索 b,需要将 b 标记为已经使用,防止重复使用。在这一次搜索结束之后,需要将 b 的已经使用状态清除,并搜索 c。
+
+
+
+本题的输入是数组而不是矩阵(二维数组),因此需要先将数组转换成矩阵。
+
```java
private final static int[][] next = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};
private int rows;
private int cols;
public boolean hasPath(char[] array, int rows, int cols, char[] str) {
- if (rows == 0 || cols == 0)
- return false;
+ if (rows == 0 || cols == 0) return false;
this.rows = rows;
this.cols = cols;
boolean[][] marked = new boolean[rows][cols];
@@ -320,14 +325,19 @@ public boolean hasPath(char[] array, int rows, int cols, char[] str) {
for (int j = 0; j < cols; j++)
if (backtracking(matrix, str, marked, 0, i, j))
return true;
+
return false;
}
-private boolean backtracking(char[][] matrix, char[] str, boolean[][] marked, int pathLen, int r, int c) {
- if (pathLen == str.length)
- return true;
- if (r < 0 || r >= rows || c < 0 || c >= cols || matrix[r][c] != str[pathLen] || marked[r][c])
+private boolean backtracking(char[][] matrix, char[] str,
+ boolean[][] marked, int pathLen, int r, int c) {
+
+ if (pathLen == str.length) return true;
+ if (r < 0 || r >= rows || c < 0 || c >= cols
+ || matrix[r][c] != str[pathLen] || marked[r][c]) {
+
return false;
+ }
marked[r][c] = true;
for (int[] n : next)
if (backtracking(matrix, str, marked, pathLen + 1, r + n[0], c + n[1]))
@@ -338,9 +348,9 @@ private boolean backtracking(char[][] matrix, char[] str, boolean[][] marked, in
private char[][] buildMatrix(char[] array) {
char[][] matrix = new char[rows][cols];
- for (int i = 0, idx = 0; i < rows; i++)
- for (int j = 0; j < cols; j++)
- matrix[i][j] = array[idx++];
+ for (int r = 0, idx = 0; r < rows; r++)
+ for (int c = 0; c < cols; c++)
+ matrix[r][c] = array[idx++];
return matrix;
}
```