StarMirror/CS-Notes
1
0
Fork 0
Code Issues Pull Requests Projects Releases Wiki Activity

auto commit

Browse Source
This commit is contained in:
CyC2018 2018-02-22 17:05:42 +08:00
parent a4035af08d
commit 60e98a0f2e
1 changed files with 4 additions and 10 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

14
notes/Leetcode 题解.md
View File

@ -1768,7 +1768,7 @@ public int minPathSum(int[][] grid) {
定义一个数组 dp 存储上楼梯的方法数（为了方便讨论，数组下标从 1 开始），dp[i] 表示走到第 i 个楼梯的方法数目。第 i 个楼梯可以从第 i-1 和 i-2 个楼梯再走一步到达，走到第 i 个楼梯的方法数为走到第 i-1 和第 i-2 个楼梯的方法数之和。 定义一个数组 dp 存储上楼梯的方法数（为了方便讨论，数组下标从 1 开始），dp[i] 表示走到第 i 个楼梯的方法数目。第 i 个楼梯可以从第 i-1 和 i-2 个楼梯再走一步到达，走到第 i 个楼梯的方法数为走到第 i-1 和第 i-2 个楼梯的方法数之和。
**dp[i] = dp[i-1] + dp[i-2]** ![](http://latex.codecogs.com/gif.latex?\\\\dp[i]=dp[i-1]+dp[i-2])
dp[N] 即为所求。 dp[N] 即为所求。
@ -1797,7 +1797,7 @@ public int climbStairs(int n) {
第 i 年成熟的牛的数量为： 第 i 年成熟的牛的数量为：
**dp[i] = dp[i-1] + dp[i-3]** ![](http://latex.codecogs.com/gif.latex?\\\\dp[i]=dp[i-1]+dp[i-3])
**强盗抢劫** **强盗抢劫**
@ -1807,7 +1807,7 @@ public int climbStairs(int n) {
定义 dp 数组用来存储最大的抢劫量，其中 dp[i] 表示抢到第 i 个住户时的最大抢劫量。由于不能抢劫邻近住户，因此如果抢劫了第 i 个住户那么只能抢劫 i - 2 和 i - 3 的住户，所以 定义 dp 数组用来存储最大的抢劫量，其中 dp[i] 表示抢到第 i 个住户时的最大抢劫量。由于不能抢劫邻近住户，因此如果抢劫了第 i 个住户那么只能抢劫 i - 2 和 i - 3 的住户，所以
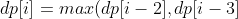**dp[i] = max(dp[i - 2], dp[i - 3]) + nums[i]** ![](http://latex.codecogs.com/gif.latex?\\\\dp[i]=max(dp[i-2],dp[i-3])+nums[i])
O(n) 空间复杂度实现方法： O(n) 空间复杂度实现方法：
@ -1999,13 +1999,7 @@ public int wiggleMaxLength(int[] nums) {
综上，最长公共子系列的状态转移方程为： 综上，最长公共子系列的状态转移方程为：
![](http://latex.codecogs.com/gif.latex?\\\\ ![](http://latex.codecogs.com/gif.latex?\\\\dp[i][j]=\left\{\begin{array}{rcl}dp[i-1][j-1]&&{S1_i==S2_j}\\max(dp[i-1][j],dp[i][j-1])&&{S1_i<>S2_j}\end{array}\right.)
dp[i][j]=\left\{
\begin{array}{rcl}
dp[i-1][j-1]&&{S1_i==S2_j}\\
max(dp[i-1][j],dp[i][j-1])&&{S1_i<>S2_j}
\end{array}\right.
)
对于长度为 N 的序列 S<sub>1</sub> 和 长度为 M 的序列 S<sub>2</sub>，dp[N][M] 就是序列 S<sub>1</sub> 和序列 S<sub>2</sub> 的最长公共子序列长度。 对于长度为 N 的序列 S<sub>1</sub> 和 长度为 M 的序列 S<sub>2</sub>，dp[N][M] 就是序列 S<sub>1</sub> 和序列 S<sub>2</sub> 的最长公共子序列长度。