diff --git a/notes/Leetcode 题解.md b/notes/Leetcode 题解.md
index 8af37740..c35d22bc 100644
--- a/notes/Leetcode 题解.md
+++ b/notes/Leetcode 题解.md
@@ -1771,6 +1771,7 @@ public int minPathSum(int[][] grid) {
+
dp[N] 即为所求。
考虑到 dp[i] 只与 dp[i - 1] 和 dp[i - 2] 有关,因此可以只用两个变量来存储 dp[i - 1] 和 dp[i - 2] 即可,使得原来的 O(n) 空间复杂度优化为 O(1) 复杂度。
@@ -1800,6 +1801,7 @@ public int climbStairs(int n) {
+
**强盗抢劫**
[Leetcode : 198. House Robber (Easy)](https://leetcode.com/problems/house-robber/description/)
@@ -1810,6 +1812,7 @@ public int climbStairs(int n) {
+
O(n) 空间复杂度实现方法:
```java
@@ -1890,6 +1893,7 @@ private int rob(int[] nums, int s, int e) {
+
dp[N] 即为所求。
和上楼梯问题一样,dp[i] 只与 dp[i-1] 和 dp[i-2] 有关,因此也可以只用两个变量来存储 dp[i-1] 和 dp[i-2]。
@@ -1906,6 +1910,7 @@ dp[N] 即为所求。
+
对于一个长度为 N 的序列,最长子序列并不一定会以 SN 为结尾,因此 dp[N] 不是序列的最长递增子序列的长度,需要遍历 dp 数组找出最大值才是所要的结果,即 max{ dp[i] | 1 <= i <= N} 即为所求。
**最长递增子序列**
@@ -2047,6 +2052,7 @@ public int lengthOfLCS(int[] nums1, int[] nums2) {
+
```java
public int knapsack(int W, int N, int[] weights, int[] values) {
int[][] dp = new int[N][W];
@@ -2071,6 +2077,7 @@ public int knapsack(int W, int N, int[] weights, int[] values) {
+
因为 dp[j-w] 表示 dp[i-1][j-w],因此不能先求 dp[i][j-w] 防止将 dp[i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w],在程序实现时需要按倒序来循环求解。
**无法使用贪心算法的解释**
diff --git a/notes/计算机网络.md b/notes/计算机网络.md
index 5e56d39c..31fa54f3 100644
--- a/notes/计算机网络.md
+++ b/notes/计算机网络.md
@@ -158,6 +158,7 @@
+
其中 l 表示数据帧的长度,v 表示发送速率。
### 2. 传播时延
@@ -166,6 +167,7 @@
+
其中 l 表示信道长度,v 表示电磁波在信道上的传播速率。
### 3. 处理时延
@@ -261,14 +263,17 @@ TCP/IP 协议族是一种沙漏形状,中间小两边大,IP 协议在其中
+
为了方便,取 m=8,设码片 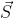 为 00011011。在拥有该码片的用户发送比特 1 时就发送该码片,发送比特 0 时就发送该码片的反码 11100100。
在计算时将 00011011 记作 (-1 -1 -1 +1 +1 -1 +1 +1),可以得到
+
+
其中
为 00011011。在拥有该码片的用户发送比特 1 时就发送该码片,发送比特 0 时就发送该码片的反码 11100100。
在计算时将 00011011 记作 (-1 -1 -1 +1 +1 -1 +1 +1),可以得到
+
+
其中 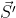 为
为 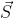 的反码。
利用上面的式子我们知道,当接收端使用码片
的反码。
利用上面的式子我们知道,当接收端使用码片 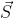 对接收到的数据进行内积运算时,结果为 0 的是其它用户发送的数据,结果为 1 的是用户发送的比特 1,结果为 -1 的是用户发送的比特 0。
@@ -668,10 +673,12 @@ TCP 使用超时重传来实现可靠传输:如果一个已经发送的报文
+
超时时间 RTO 应该略大于 RRTs,TCP 使用的超时时间计算如下:
+
其中 RTTd 为偏差,它与新的 RRT 和 RRTs 有关。
## TCP 流量控制
对接收到的数据进行内积运算时,结果为 0 的是其它用户发送的数据,结果为 1 的是用户发送的比特 1,结果为 -1 的是用户发送的比特 0。
@@ -668,10 +673,12 @@ TCP 使用超时重传来实现可靠传输:如果一个已经发送的报文
+
超时时间 RTO 应该略大于 RRTs,TCP 使用的超时时间计算如下:
+
其中 RTTd 为偏差,它与新的 RRT 和 RRTs 有关。
## TCP 流量控制