diff --git a/notes/Leetcode 题解 - 动态规划.md b/notes/Leetcode 题解 - 动态规划.md
index 305174be..643b0dc7 100644
--- a/notes/Leetcode 题解 - 动态规划.md
+++ b/notes/Leetcode 题解 - 动态规划.md
@@ -1055,7 +1055,10 @@ public int combinationSum4(int[] nums, int target) {
题目描述:交易之后需要有一天的冷却时间。
-
+
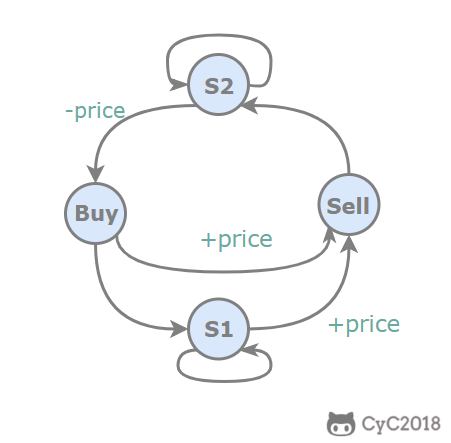
+该题为马尔可夫过程,分为A观望,B持股,C冷却三个状态
+状态转移图:A-(观望)->A, A-(买入|-price)->B, B-(观望)->B, B-(卖出|+price)->C, C-(冷却)->A
+可用维特比算法求解
```java
public int maxProfit(int[] prices) {
@@ -1063,19 +1066,17 @@ public int maxProfit(int[] prices) {
return 0;
}
int N = prices.length;
- int[] buy = new int[N];
- int[] s1 = new int[N];
- int[] sell = new int[N];
- int[] s2 = new int[N];
- s1[0] = buy[0] = -prices[0];
- sell[0] = s2[0] = 0;
+ int[] A = new int[N];
+ int[] B = new int[N];
+ int[] C = new int[N];
+ A[0] = 0;
+ B[0] = C[0] = -prices[0];
for (int i = 1; i < N; i++) {
- buy[i] = s2[i - 1] - prices[i];
- s1[i] = Math.max(buy[i - 1], s1[i - 1]);
- sell[i] = Math.max(buy[i - 1], s1[i - 1]) + prices[i];
- s2[i] = Math.max(s2[i - 1], sell[i - 1]);
+ A[i] = Math.max(A[i - 1], C[i - 1]);
+ B[i] = Math.max(B[i - 1], A[i - 1] - prices[i]);
+ C[i] = B[i - 1] + prices[i];
}
- return Math.max(sell[N - 1], s2[N - 1]);
+ return Math.max(A[N - 1], C[N - 1]);
}
```
@@ -1098,24 +1099,22 @@ The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.
题目描述:每交易一次,都要支付一定的费用。
-
+
+分为A观望,B持股,两个状态
+状态转移图:A-(观望)->A, A-(买入|-price)->B, B-(观望)->B, B-(卖出|+price|-fee)->A
```java
public int maxProfit(int[] prices, int fee) {
int N = prices.length;
- int[] buy = new int[N];
- int[] s1 = new int[N];
- int[] sell = new int[N];
- int[] s2 = new int[N];
- s1[0] = buy[0] = -prices[0];
- sell[0] = s2[0] = 0;
+ int[] A = new int[N];
+ int[] B = new int[N];
+ A[0] = 0;
+ B[0] = -prices[0];
for (int i = 1; i < N; i++) {
- buy[i] = Math.max(sell[i - 1], s2[i - 1]) - prices[i];
- s1[i] = Math.max(buy[i - 1], s1[i - 1]);
- sell[i] = Math.max(buy[i - 1], s1[i - 1]) - fee + prices[i];
- s2[i] = Math.max(s2[i - 1], sell[i - 1]);
+ A[i] = Math.max(A[i - 1], B[i - 1] + prices[i] -fee);
+ B[i] = Math.max(A[i - 1] - prices[i], B[i - 1]);
}
- return Math.max(sell[N - 1], s2[N - 1]);
+ return A[N - 1];
}
```